5 Basic Math Properties
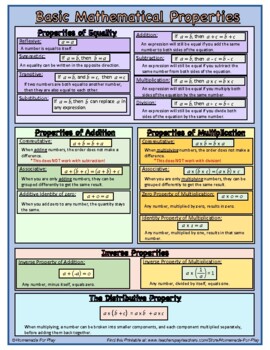
Understanding the fundamental properties of mathematics is crucial for building a strong foundation in the subject. Among these properties, there are five that stand out for their universality and importance across various mathematical operations: the Commutative Property, the Associative Property, the Distributive Property, the Identity Property, and the Inverse Property.
Commutative Property
The Commutative Property states that the order of the numbers being added or multiplied does not change the result. This property applies to both addition and multiplication. For example:
- Addition: (a + b = b + a)
- Multiplication: (a \times b = b \times a)
To illustrate, consider the numbers 3 and 5:
- Addition: (3 + 5 = 5 + 3 = 8)
- Multiplication: (3 \times 5 = 5 \times 3 = 15)
This property makes it easier to rearrange numbers in calculations to simplify them or make mental math easier.
Associative Property
The Associative Property focuses on how numbers are grouped during addition or multiplication. It asserts that the way in which numbers are grouped (or associated) does not affect the outcome of the operation. This property is also applicable to both addition and multiplication. For example:
- Addition: ((a + b) + c = a + (b + c))
- Multiplication: ((a \times b) \times c = a \times (b \times c))
Using the same numbers, 3 and 5, and adding a third number, 2:
- Addition: ((3 + 5) + 2 = 8 + 2 = 10) and (3 + (5 + 2) = 3 + 7 = 10)
- Multiplication: ((3 \times 5) \times 2 = 15 \times 2 = 30) and (3 \times (5 \times 2) = 3 \times 10 = 30)
This property is essential for simplifying expressions by allowing the regrouping of numbers.
Distributive Property
The Distributive Property, often referred to as the distributive law, states that for any numbers (a), (b), and (c), the following holds:
- Distributive over addition: (a(b + c) = ab + ac)
- Distributive over subtraction: (a(b - c) = ab - ac)
To illustrate with an example, let’s use (a = 3), (b = 5), and (c = 2):
- Over addition: (3(5 + 2) = 3 \times 7 = 21) and (3 \times 5 + 3 \times 2 = 15 + 6 = 21)
- Over subtraction: (3(5 - 2) = 3 \times 3 = 9) and (3 \times 5 - 3 \times 2 = 15 - 6 = 9)
This property is invaluable for expanding and simplifying algebraic expressions.
Identity Property
The Identity Property introduces the concept of an identity element, which does not change the result when it is added to or multiplied by another number. For addition, the identity element is 0 (since (a + 0 = a)), and for multiplication, the identity element is 1 (since (a \times 1 = a)).
- Additive Identity: (a + 0 = a)
- Multiplicative Identity: (a \times 1 = a)
Using (a = 4) as an example:
- Additive Identity: (4 + 0 = 4)
- Multiplicative Identity: (4 \times 1 = 4)
This property ensures that there is a starting point or a “neutral” element in both addition and multiplication, which is crucial for solving equations and manipulating expressions.
Inverse Property
The Inverse Property deals with the relationship between a number and its inverse. For addition, the inverse of (a) is (-a) (since (a + (-a) = 0)), and for multiplication, the inverse of (a) is (1/a) (since (a \times 1/a = 1)).
- Additive Inverse: (a + (-a) = 0)
- Multiplicative Inverse: (a \times 1/a = 1)
Taking (a = 5) as an example:
- Additive Inverse: (5 + (-5) = 0)
- Multiplicative Inverse: (5 \times 1⁄5 = 1)
This property is vital for solving equations and understanding how to “undo” operations to isolate variables.
Conclusion
These five basic math properties - Commutative, Associative, Distributive, Identity, and Inverse - form the backbone of arithmetic and algebra. They provide a framework for understanding how numbers interact with each other under different operations, allowing us to simplify complex expressions, solve equations, and develop a deeper understanding of mathematical structures. Whether you’re a student looking to grasp the fundamentals or a professional seeking to refine your mathematical tools, mastering these properties is essential for advancing in mathematics and applying mathematical concepts to real-world problems.
Frequently Asked Questions
What is the purpose of the Commutative Property in mathematics?
+The Commutative Property allows for the rearrangement of numbers in addition and multiplication operations without changing the result, making calculations more flexible and easier to perform mentally.
How does the Distributive Property help in algebra?
+The Distributive Property is crucial in algebra for expanding and simplifying expressions, allowing for the multiplication of a single term over several terms within parentheses, which is essential for solving equations and simplifying complex algebraic expressions.
What role do Identity Elements play in mathematics?
+Identity Elements (0 for addition and 1 for multiplication) serve as the “neutral” elements, providing a starting point for operations and allowing for the concept of a “do nothing” operation, which is vital for defining the results of operations involving zero or one.
Can you explain the practical application of the Inverse Property?
+The Inverse Property is practically applied in solving equations and “undoing” operations. For example, to isolate a variable, one might use its inverse to cancel it out. This property is fundamental in algebra and is used extensively in solving linear and non-linear equations.
How does understanding these properties help in real-world applications?
+Understanding these fundamental properties enhances problem-solving skills, allowing for more efficient and accurate calculations. This proficiency is beneficial in various real-world applications, including science, engineering, economics, and computer science, where mathematical models and equations are used to describe and predict phenomena.

