Standard Deviation 68 95 99 Rule
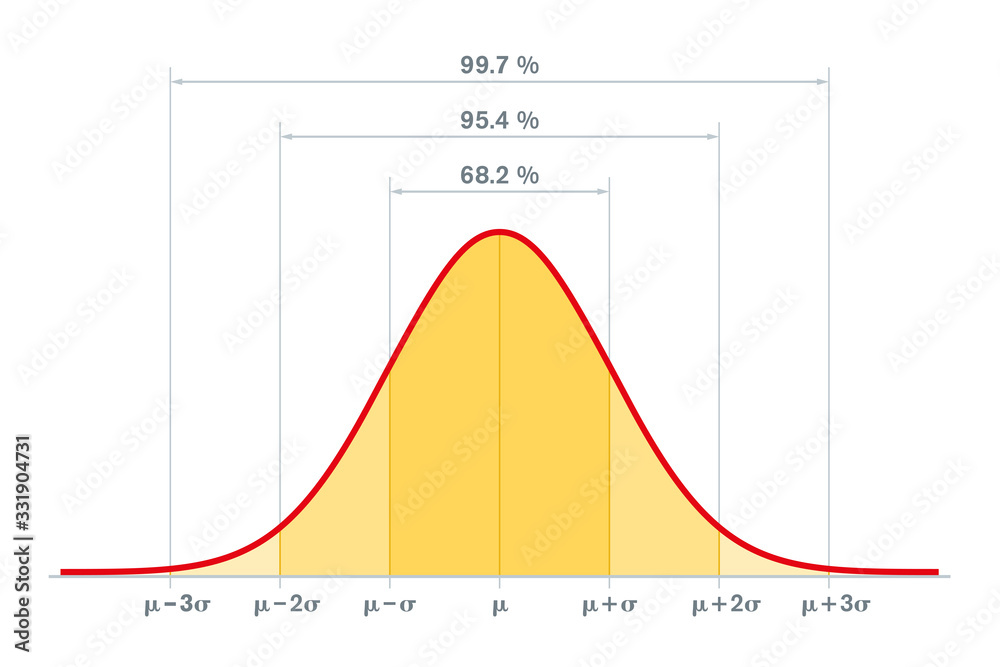
Understanding the concept of standard deviation is crucial in statistics, as it measures the amount of variation or dispersion in a set of values. A key principle in understanding standard deviation is the 68-95-99 rule, also known as the empirical rule. This rule provides a guideline for the percentage of data points that fall within a certain range of standard deviations from the mean.
Introduction to Standard Deviation
Standard deviation is a measure that is used to quantify the amount of variation or dispersion of a set of data values. A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range.
The 68-95-99 Rule
The 68-95-99 rule states that for a normal distribution (a distribution that is symmetric and bell-shaped), nearly all of the data will fall within three standard deviations of the mean. More specifically, the rule states: - About 68% of the data falls within one standard deviation of the mean. - About 95% of the data falls within two standard deviations of the mean. - About 99.7% of the data falls within three standard deviations of the mean.
This rule is a simplification of the more precise 68-95-99.7 rule but serves as a practical approximation for understanding how data points distribute around the mean in a normal distribution.
Understanding the Rule
To understand this rule better, consider a scenario where we are analyzing the heights of a large population of adults. Let’s say the mean height is 175 cm with a standard deviation of 5 cm. - According to the rule, about 68% of adults would have a height between 170 cm and 180 cm (mean ± 1 standard deviation). - About 95% would have a height between 165 cm and 185 cm (mean ± 2 standard deviations). - And about 99.7% would have a height between 160 cm and 190 cm (mean ± 3 standard deviations).
Practical Applications
This rule has numerous practical applications across various fields: - Finance: Investors use standard deviation to measure the volatility of stock prices or portfolio returns, helping them understand the risk associated with their investments. - Quality Control: Manufacturers use the 68-95-99 rule to set acceptable limits for product dimensions, ensuring that most products fall within a specific range. - Medicine: The rule can help in understanding the distribution of characteristics like blood pressure or cholesterol levels among a population.
Limitations and Considerations
While the 68-95-99 rule is incredibly useful, it’s essential to remember that it applies most accurately to normal distributions. Many real-world datasets do not follow a perfect normal distribution, and in such cases, the rule serves more as a guideline than a precise predictor.
Additionally, the rule does not apply well to skewed distributions or those with outliers, as these can significantly affect the mean and standard deviation, leading to inaccurate predictions of data distribution.
Conclusion
The 68-95-99 rule provides a foundational understanding of how data distributes around the mean in a normal distribution. Its applications are vast, ranging from finance to quality control, and it serves as a critical tool for data analysis and interpretation. However, it’s crucial to consider the nature of the data distribution before applying this rule, as deviations from normality can affect its accuracy.
What does the 68-95-99 rule imply about data distribution?
+The 68-95-99 rule implies that in a normal distribution, about 68% of the data points fall within one standard deviation of the mean, about 95% fall within two standard deviations, and about 99.7% fall within three standard deviations.
Is the 68-95-99 rule applicable to all types of data distributions?
+No, the 68-95-99 rule is most accurately applied to normal distributions. For skewed distributions or those with significant outliers, the rule may not provide a precise prediction of data distribution.
What are some practical applications of the 68-95-99 rule?
+The rule has applications in finance for measuring investment risk, in quality control for setting product specification limits, and in medicine for understanding the distribution of health metrics among a population.
In conclusion, the 68-95-99 rule is a powerful tool for understanding and analyzing data, with a wide range of applications across different fields. Its ability to provide insights into how data points distribute around the mean makes it an indispensable principle in statistics and data analysis.