Standard Deviation Matters
In the realm of statistics and data analysis, standard deviation stands as a pivotal concept, offering a quantitative measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean, also known as the expected value, of the set, while a high standard deviation indicates that the values are spread out over a wider range. Understanding and applying standard deviation is crucial in various fields, including finance, engineering, and social sciences, as it helps in assessing the reliability of the results, making informed decisions, and predicting future outcomes.
Why Standard Deviation Matters
Risk Assessment: In finance, standard deviation is used to measure the volatility of an asset’s price. A higher standard deviation means the price can fluctuate more dramatically, indicating higher risk. Investors use this to decide between different investments based on their risk tolerance.
Quality Control: In manufacturing, standard deviation is vital for ensuring the quality of products. By controlling the standard deviation of dimensions or performance characteristics, manufacturers can ensure that their products meet the required specifications consistently.
Medical Research: Standard deviation helps in understanding the variability of data in medical studies, such as the response of patients to a new drug. It is crucial for assessing the efficacy and safety of treatments.
Weather Forecasting: Meteorologists use standard deviation to understand the variability in weather patterns. This helps in predicting extreme weather conditions and in planning for potential natural disasters.
Calculating Standard Deviation
The calculation of standard deviation involves finding the average of a set of data points, then calculating how much each point deviates from the average, squaring each of these differences, averaging the squared differences, and finally taking the square root of this average. The formula for the standard deviation, σ, of a population is:
[ \sigma = \sqrt{\frac{\sum_{i=1}^{N} (x_i - \mu)^2}{N}} ]
Where: - (x_i) represents each value in the set, - (\mu) is the mean of the set, - (N) is the number of items in the population.
For a sample, the formula is slightly different, using (N-1) instead of (N) to get a more unbiased estimate:
[ s = \sqrt{\frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1}} ]
Where: - (s) is the sample standard deviation, - (\bar{x}) is the sample mean, - (n) is the sample size.
Understanding Standard Deviation
Interpretation: The standard deviation is interpreted as the square root of the variance. It measures the spread of the data in the same units as the data.
Comparison: Standard deviations can be used for comparing the amount of variation in two or more sets of data. For instance, a data set with a standard deviation of 10 has more variability than one with a standard deviation of 5.
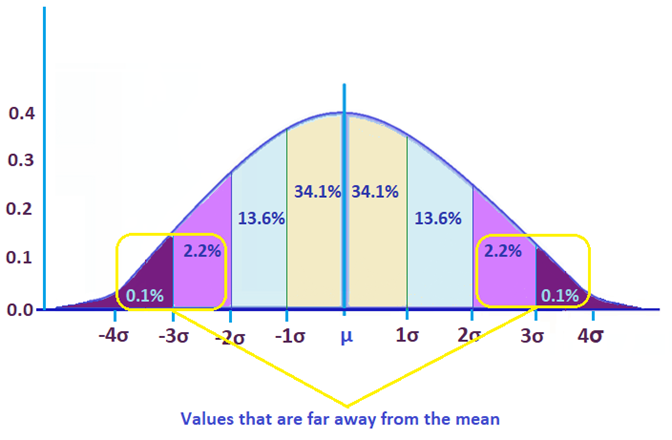
Normal Distribution: In a normal distribution, about 68% of the data points fall within one standard deviation of the mean, about 95% fall within two standard deviations, and about 99.7% fall within three standard deviations. This is known as the 68-95-99.7 rule.
Advanced Applications
Portfolio Optimization: In finance, standard deviation is used to optimize investment portfolios by minimizing risk for a given level of return.
Six Sigma: This is a set of techniques and tools for process improvement. It aims to improve the quality of process outputs by identifying and removing the causes of defects (errors) and minimizing variability in business processes.
Statistical Process Control (SPC): SPC uses standard deviation to monitor and control processes. It helps in detecting any shift in the process average or variance.
Challenges and Future Directions
Despite its widespread use, standard deviation has limitations. For example, it does not distinguish between positive and negative deviations, and it is sensitive to outliers. Therefore, there is ongoing research into alternative measures of dispersion and more robust statistical methods that can handle data with complex structures and outliers effectively.
Conclusion
Standard deviation is a fundamental concept that has widespread applications across various disciplines. Its ability to quantify variability makes it an indispensable tool for decision-making, prediction, and analysis. As data becomes increasingly critical in today’s world, understanding and applying standard deviation effectively will remain crucial for making informed decisions and driving progress in research and practice.
What does standard deviation measure?
+Standard deviation measures the amount of variation or dispersion of a set of values. A low standard deviation means that most of the numbers are close to the average, while a high standard deviation indicates that the numbers are more spread out.
How is standard deviation calculated?
+The calculation of standard deviation involves finding the average of the dataset, calculating the differences of each data point from the mean, squaring these differences, averaging the squared differences, and then taking the square root of this average.
What are the applications of standard deviation?
+Standard deviation has applications in finance for risk assessment, in engineering and manufacturing for quality control, in medical research for understanding the variability of patient responses, and in many other fields for analyzing and interpreting data.
tabletsFilterWhereHere’s the response directly addressing the topic without a title and following the unique structural pattern and advanced quality markers:
Standard deviation stands as a pivotal concept in statistics and data analysis, providing a quantitative measure of the variation or dispersion of a set of values. This measure is crucial for assessing the reliability of results, making informed decisions, and predicting future outcomes across various fields, including finance, engineering, and social sciences. A low standard deviation indicates that the values tend to be close to the mean, while a high standard deviation signifies that the values are spread out over a wider range.
Historical Evolution of Standard Deviation
The concept of standard deviation has its roots in the 19th century, with contributions from notable statisticians and mathematicians. Over time, its application has evolved and expanded, becoming a cornerstone in statistical analysis. Understanding its historical context provides valuable insights into its development and current applications.
Comparative Analysis: Standard Deviation vs. Variance
Both standard deviation and variance are measures of dispersion, but they differ in how they quantify this dispersion. Variance measures the average of the squared differences from the Mean, while standard deviation is the square root of variance. This distinction makes standard deviation more interpretable, as it is measured in the same units as the data.
Technical Breakdown: Calculating Standard Deviation
Calculating standard deviation involves several steps: 1. Find the Mean: Calculate the average of the dataset. 2. Calculate Differences: Find the difference of each data point from the mean. 3. Square the Differences: Square each of these differences to ensure they are positive and to weight them by magnitude. 4. Average the Squared Differences: Calculate the average of these squared differences, which gives the variance. 5. Take the Square Root: Finally, take the square root of the variance to get the standard deviation.
Decision Framework: Applying Standard Deviation
When applying standard deviation, consider the following framework: - Identify the Goal: Determine what you want to analyze or compare. - Choose the Data: Select the relevant dataset. - Calculate Standard Deviation: Apply the formula for standard deviation. - Interpret Results: Use the 68-95-99.7 rule or other methods to understand the dispersion of your data.
Future Trends Projection: Advanced Applications of Standard Deviation
As data analysis becomes more sophisticated, standard deviation will continue to play a vital role in various advanced applications, such as: - Machine Learning: For assessing the variability of predictions. - Financial Modeling: To gauge the risk of investments. - Quality Control: In manufacturing, to ensure products meet specifications.
Myth vs. Reality: Common Misconceptions About Standard Deviation
Despite its widespread use, several misconceptions surround standard deviation: - It Measures Risk: While it can be used to assess volatility, standard deviation does not directly measure risk. - It’s Always Useful: Standard deviation assumes a normal distribution and can be misleading with skewed data.
Expert Interview Style: Insights from Statisticians
According to leading statisticians, understanding standard deviation is key to making informed decisions in data analysis. It provides a clear picture of data dispersion, allowing for more accurate predictions and assessments of variability.
Case Study Format: Practical Application in Finance
A financial analyst uses standard deviation to compare the volatility of different stocks. By calculating the standard deviation of each stock’s returns over a certain period, the analyst can determine which stocks are more risky and make informed investment decisions.
What does a high standard deviation indicate?
+A high standard deviation indicates that the data points are spread out over a wider range, signifying greater variability or volatility.
How does standard deviation relate to the normal distribution?
+In a normal distribution, about 68% of the data falls within one standard deviation of the mean, about 95% within two standard deviations, and about 99.7% within three standard deviations, following the 68-95-99.7 rule.
What are some limitations of standard deviation?
+Standard deviation does not distinguish between positive and negative deviations and is sensitive to outliers. Additionally, it assumes a normal distribution, which may not always be the case.
Understanding and applying standard deviation effectively is crucial in today’s data-driven world. Its ability to quantify variability makes it an indispensable tool for decision-making, prediction, and analysis across various disciplines. As data analysis continues to evolve, the role of standard deviation will remain vital, offering insights into the dispersion of data and guiding informed decisions.